Python : 순열(Permutation) Review
완전탐색을 할 때 주로 쓰이는 파트이므로 꼭 알아야하므로 한번 더 리뷰하려고 한다. 물론 재귀를 사용하는 중요한 방법이고 중복순열과 일반 순열이 있으니 두개 다 알아보도록 하자.
순열(Permutation)이란?
- 서로 다른 N개에서, R개를 중복없이 순서를 고려하여 나열한 것 [경우의 수 = N * (N - 1) * (N - 2) ... (N - R + 1)]
예를들어 0, 1, 2 로 구성된 3장의 카드들이 여러장 존재하는데, 이 중 2장을 뽑아 순열을 나열해 보자. 그렇다면 해당하는 순열은 [0 1] [0 2] [1 0] [1 2] [2 0] [2 1] 으로 총 6개임을 알 수 있다.
- 중복순열은 서로다른 N개에서 R개를 중복 허용, 순서를 고려하여 나열하는 것 [경우의 수 = N**R]
위와 같은 예시로 보면, 중복 순열은 [0 0] [0 1] [0 2] [1 0] [1 1] [1 2] [2 0] [2 1] [2 2] 로 총 9개임을 알 수 있다.
순열의 구현 원리
- 재귀호출을 할 때 마다, 이동 경로를 흔적(path)으로 남긴다
- 가장 마지막 레벨에 도착했을 때, 이동 경로를 출력한다

이제 이동경로를 추적하기 위해 path의 list에 경로를 기록해보자.
path = []
def plus(n):
if n == 2:
return
for i in range(3):
path.append(i)
plus(n + 1)
plus(0)

이전 포스팅에서 계속 보던 예시이다. level은 2이고, branch는 3인 예시이며, 한번 진행 했다면 위와 같다.

이렇게 첫 path를 찾아냈고, 이후 다음 재귀는 Main으로 돌아오는 것이 아니라 깊어져 있는 재귀에서 반복문을 진행 하는 것이다.



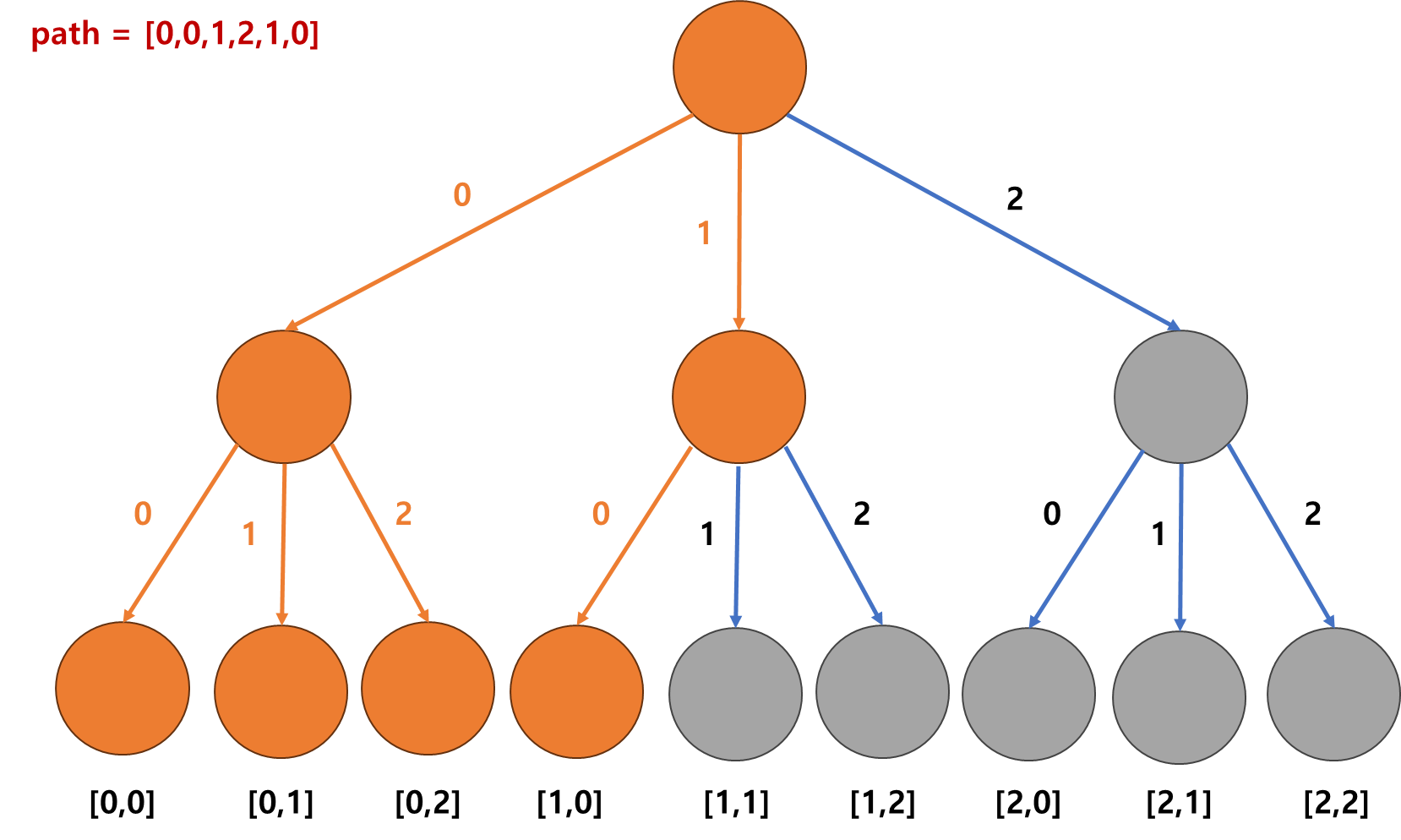

그런데 우리가 원하는 것은 path = [0, 0, 1, 2, 1, 0, 1, 2, 2, 0, 1 ,2] 가 아니라
path = [0, 0], [0, 1] [0, 2] [1, 0] [1, 1] [1, 2] [2, 0] [2, 1] [2, 2]를 원한다. 이때 넣어줘야하는 print(n)의 위치와 path에서 되돌아 갈 때, 재귀하면서 path의 흔적을 pop() 함수로 통해 제거시켜주면 가능하다.
path = []
def plus(n):
if n == 2:
print(path)
return
for i in range(3):
path.append(i)
plus(n + 1)
path.pop()
plus(0)
'''
[0, 0]
[0, 1]
[0, 2]
[1, 0]
[1, 1]
[1, 2]
[2, 0]
[2, 1]
[2, 2]
'''


이렇게 반복문과 재귀를 모두 마지막까지 진행 된다면,

그렇다면 기저조건에 달성된 path의 깊이가 2일때 재귀되므로 기저조건 내에 print()를 찍어본다면 내가 원하는 결과를 얻을 수 있을 것이다.
path = []
def plus(n):
if n == 2:
print(path)
return
for i in range(3):
path.append(i)
plus(n + 1)
path.pop()
plus(0)
'''
[0, 0]
[0, 1]
[0, 2]
[1, 0]
[1, 1]
[1, 2]
[2, 0]
[2, 1]
[2, 2]
'''
다른 예시를 풀어보자. 숫자 카드는 1~6까지 있고 총 3개를 나열한다고 하면, branch는 6, level은 3이다. 코드로 나타내면 아래와 같다.
path = []
def permutation(n):
if len(path) == 3:
print(path)
return
for i in range(1, 7):
path.append(i)
permutation(n+1)
path.pop()
permutation(0)
코드에는 permutation(0)으로 들어가있지만, 없어도 가능하다. 어차피 branch와 level은 명시되어 있기 때문에 아래의 코드와도 같다
path = []
def permutation():
if len(path) == 3:
print(path)
return
for i in range(1, 7):
path.append(i)
permutation()
path.pop()
permutation()이번에는 중복이 없는 순열을 만들어 보자.
위에 중복을 포함한 순열에서 중복을 제거하는 코드를 추가하면 순열 코드로 변형할 수 있다.
이때, 전역 리스트인 이미 선택했던 숫자인지 아닌지 구분하는 used 배열 또는 visited 배열을 사용한다.
DFS, BFS에 사용되는 것과 동일하다
해결하는 방법을 생각해보면, 재귀 호출을 하기 직전에 그 호출할 n이 이미 선택했던 숫자인지 아닌지 검사하는 코드를 작성한다. 이미 사용된 숫자라면 continue를 통해 스킵을 하면 된다.
그렇다면 사용한 숫자인지 아닌지 확인하는 list를 준비해보자. (나는 주로 visited라고 짓는데, used가 쓰기 편해보인다)
used_1 = [False, False, False]
used_2 = [False for _ in range(3)]
print(used_1)
print(used_2)
'''
[False, False, False]
[False, False, False]
'''
만드는 방법은 보통 리스트컨프리핸션을 사용하는 것이 편리하다. 만들어줄 False의 개수는 branch의 값과 동일하다. 또한 인덱스로 접근하므로 헷갈리지 않도록 한다. 만약 사용되었다면, True로 바꿔줄 예정이다.
path = []
used = [False for _ in range(3)]
def permutation(n):
if n == 2:
print(path)
return
for i in range(3):
if used[i] == False:
path.append(i)
permutation(n+1)
path.pop()
else:
continue
permutation(0)
used 배열을 추가해주었고, 함수 안 반복문에 조건문을 추가하여 used가 False경우 실행, True경우 skip을 해준다. 하지만 위의 코드는 미완성이다. 왜냐?? used가 True 가 되는 식을 넣어주지 않았다.
그럼 생각해보자, 어디다 넣어야 할까??
False인지 확인한 후에 실행되는 부분이라면, 바로 False를 True로 바꿔주는 것이 들어가면 좋을 것 같다. 반대로 재귀가 실행되고 돌아온다면 path에서 pop()하는데, 동일하게 used 역시 True에서 False로 되돌려줘야하지 않을까??
그렇다면 추가되어야할 코드는 두가지다.
path = []
used = [False for _ in range(3)]
def permutation(n):
if n == 2:
print(path)
return
for i in range(3):
if used[i] == False:
used[i] = True
path.append(i)
permutation(n+1)
path.pop()
used[i] = False
else:
continue
permutation(0)
함수의 반복문 내에 있는 조건문을 실행할테니, 실행되었다면 used[i]를 True로 바꿔주고, 재귀가 끝난 후 빠져나올때, path.pop()을 실행할테니 그와 동시에 used[i] = False로 되돌려주면 된다.
이 과정을 기록 / 삭제로 부르는 사람이 있고 결정 / 복구 라고 부르는 사람이 있으니 편한대로 하면 될 듯 하다.
마지막 복습으로 중복 순열을 만드는 것과 순열을 구해보자.
예시로, 숫자 1~13까지 적힌 카드가 무수히 있을 때, 3개를 골랐을 때의 경우를 모두 구해보자.
3개를 고를때 같은 숫자를 고를 수 있으므로 중복순열임을 확인하고 코드를 작성하면 된다. 중복순열에서는 중복이 허용되기 때문에 used와 같은 list는 사용할 필요 없고, 총 3개를 뽑으며 13개의 숫자가 있으니, level은 3, branch는 13이라고 보면 된다. 그렇다면 결국 똑같다. 만들어보자! 아참, 이번에는 경우의 수까지 확인해보자. 물론 13개의 숫자 3번을 뽑는거니 13* 13* 13 이지만, count를 사용하여 출력해보려 한다.
path = []
cnt = 0
def card(n):
global cnt
if n == 3:
print(path)
cnt += 1
return
for i in range(1, 14):
path.append(i)
card(n+1)
path.pop()
card(0)
print(cnt) # 2197
n == 3일때 path를 출력하니, 해당 위치에 cnt += 1 을 작성해주면 최종 cnt의 출력값은 2197로 13*13*13의 값인 2197과 동일한 것을 확인할 수 있다.
이번에는 순열을 만들어보자.
같은 숫자를 고를 수 없으므로 used 배열이 필요하다는 것을 인지, 총 카드 숫자는 13개가 있으므로 어떤 상황에서 used 배열이 변화하는지 확인하고 조건문을 추가해야 하는 것을 인지하자. 총 4가지가 추가된다.
여기서 주의해야할 점은 무작정 used 의 False 배열을 13개 만드는 것이 아니다, 숫자로 확인할 것이라면 13까지 나오게 되므로 반복문에 for i in range(1,14)를 사용하게 될텐데, False 배열은 index로 접근하기 때문에 잘못하면 out of range가 나오게 된다. 따라서 메모리가 부족한 것이아니라면 타이트하게 하지 않고, 여유있게 생성하면 좋다.
가장 좋은 방법은 들어갈 데이터의 가장 큰 수를 기준으로 +1 하여 배열을 생성하는 것도 하나의 방법이다.
path = []
used = [False for _ in range(14)]
cnt = 0
def card(n):
global cnt
if n == 3:
print(path)
cnt += 1
return
for i in range(1, 14):
if used[i] == False:
used[i] = True
path.append(i)
card(n+1)
path.pop()
used[i] = False
card(0)
print(cnt) # 1716
역시 count 해보니 13 * 12 * 11의 값인 경우의 수 1716이 나오는 것을 확인할 수 있다.
경우의 따라 used 배열은 False 말고도 0이나 -1을 채우는 경우가 있으니 문제에 적합하게 사용하는 것이 가장 중요하다.
복습을하면서 새로운 것을 알아가기도 하고, 까먹은 것도 다시 복습하니 웬만한 쉬운 문제는 깔끔하게 해결이 가능한 것 같다. 물론 문제로 부딪히면 여전히 기절한다.