Python : 깊이 우선 탐색(Depth First Search, DFS) (1)

가장 처음 파이썬을 공부할 때 다른 친구들이 알고리즘 문제 풀고 있는것을 들었을때 무슨 전문용어마냥 'DFS로 푸는거야?' 이럴때부터 쫄아있던 단원이다. 굉장히 어려워보이는 단어처럼 보이지 않는가? 정답이다. 서론을 간단하게 풀자면 비선형구조인 그래프 구조는 그래프로 표현된 모든 자료를 빠짐없이 검색하는 것이 중요하다. 

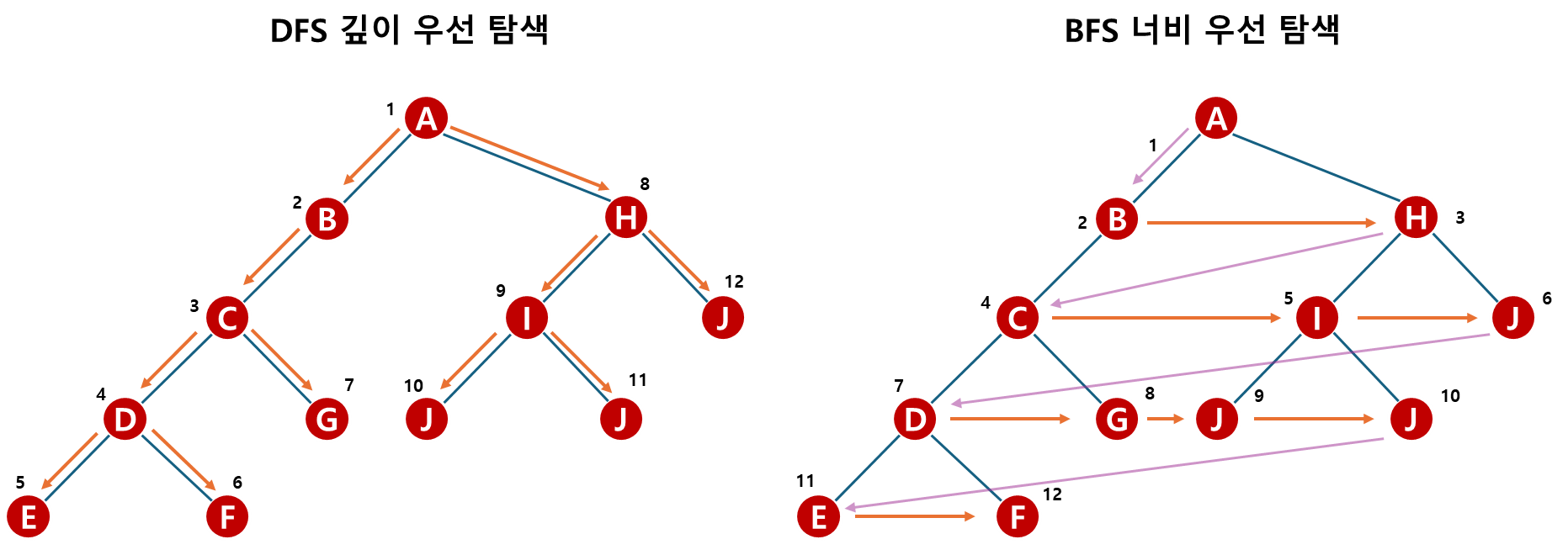
깊이 우선 탐색(DFS) 와 너비 우선 탐색 (Breadth First Search, BFS) 총 두가지 방법이 있으며 오늘은 DFS에 대해 알아볼 것이다.

---

깊이 우선 탐색(Depth First Search, DFS)

: 시작 정점의 한 방향으로 갈 수 있는 경로가 있는 곳(가장 깊은 곳)까지 깊이 탐색해 가다가 더이상 갈 곳이 없게 되면, 가장 마지막에 만났던 갈림길 간선이 있는 정점으로 되돌아와서 다른 방향의 정점으로 탐색을 계속 반복하여 결국 모든 정점을 방문하는 순회 방법

이러한 방식 때문에 stack 이나 recursion을 이용해 구현이 가능하다

가장 마지막에 만났던 갈림길의 정점으로 되돌아가서 다시 깊이 우선 탐색을 반복해야 하므로 후입 선출 구조의 Stack을 사용한다.

 

장점 : 메모리 효율성이 좋음. 

방문한 노드의 스택만 유지하면 되기 때문에 BFS에 비해 적은 메모리를 사용한다.

 

단점 : 최단경로는 적합하지 않음.

완전탐색 및 그래프의 모든 경로를 탐색하기 때문에 가장 먼저 찾은 경로가 최단 경로임을 확정지을 수 없다. 이럴 경우 BFS 혹은 다익스트라(Dijkstra) 알고리즘이 더 적합하다.

 

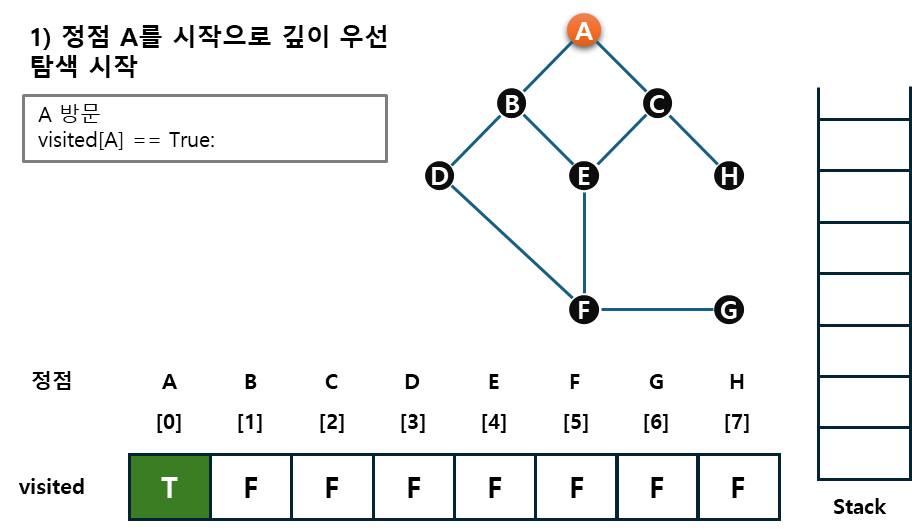
1) 시작 정점 v를 결정하여 방문

 

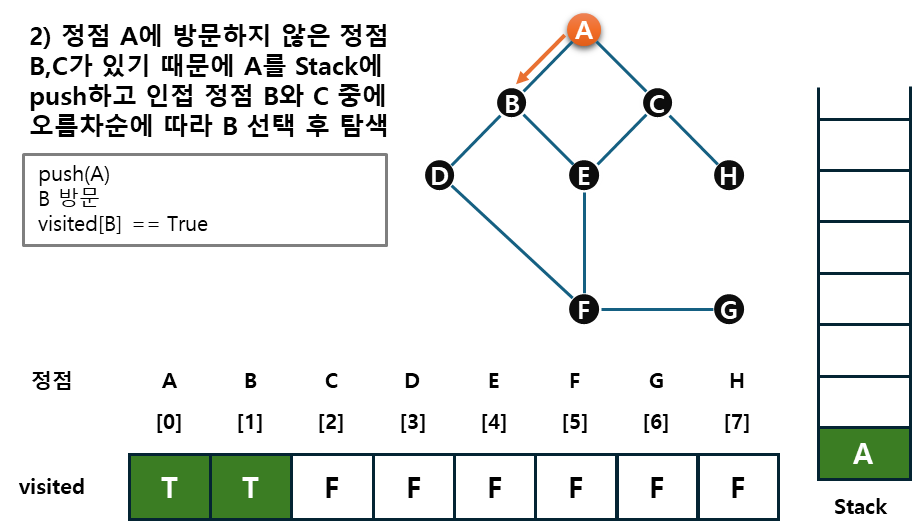
2) 정점 v에 인접한 정점 중에서

1. 탐색단계 : 방문 하지 않은 정점 w가 있으면, 정점 v를 스택에 추가(push)하고 정점 w를 방문한다. 그리고 w를 v로 하여 다시 2)를 반복한다. 
2. 후퇴단계 : 방문하지 않은 정점이 없으면, 탐색의 방향을 바꾸기 위해서 스택을 제거(pop)하여 받은 가장 마지막 방문 정점 v로 하여 다시 2)를 반복한다.

3) Stack이 공백이 될 때까지 2)를 반복

 

활용 : 그래프의 연결성을 테스트하는 데 사용이 가능 (경로 찾기, 사이클 감지, 그래프 분리 구성요소 찾기 등)

 

DFS와 BFS의 탐색 순서

 

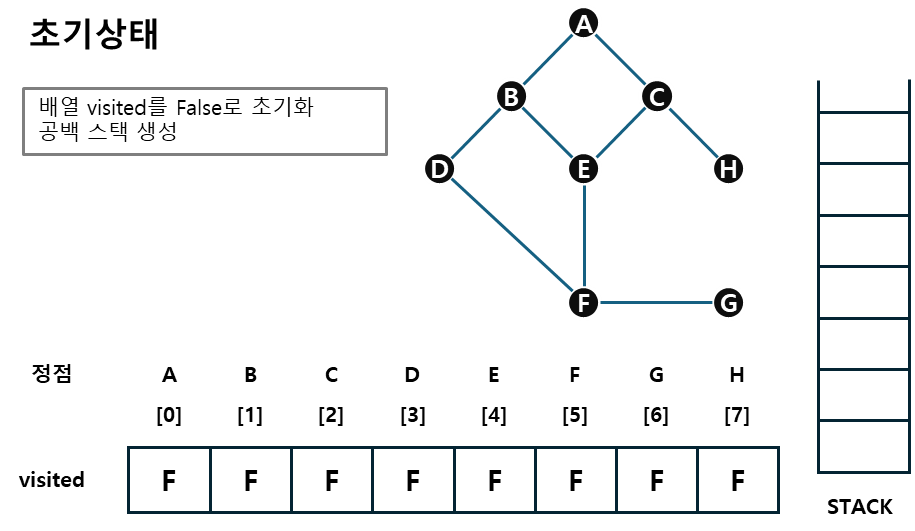
예시를 통해 그래프, stack, visited를 살펴보자.

---

---

 

---

---

 

---

---

---

---

---

---

---

---

---

---

---

---

---

 

 

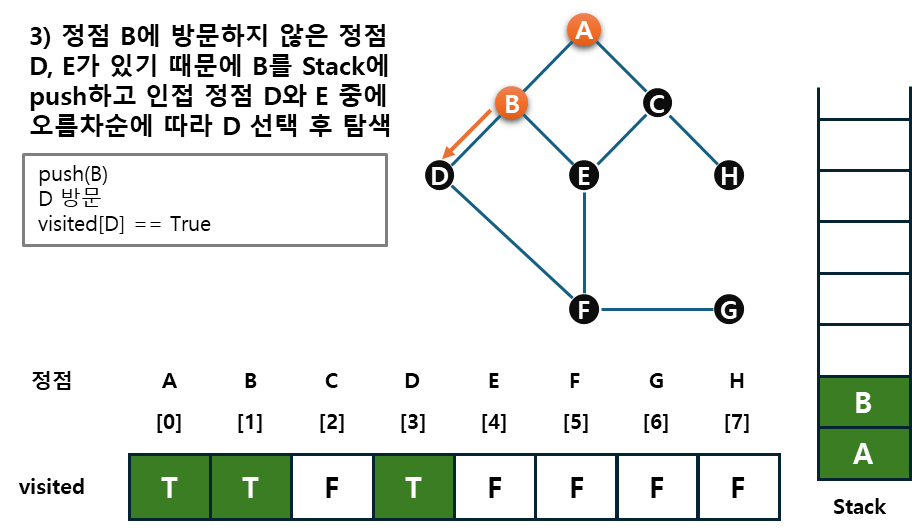
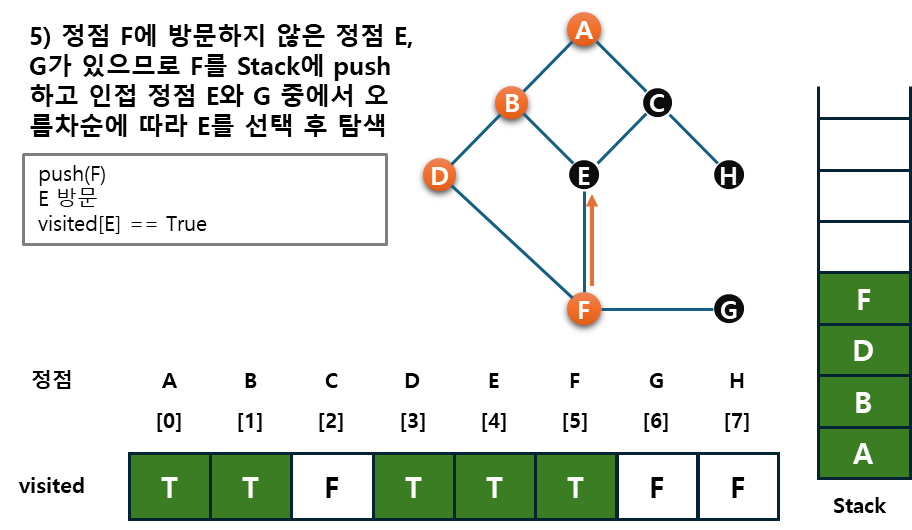
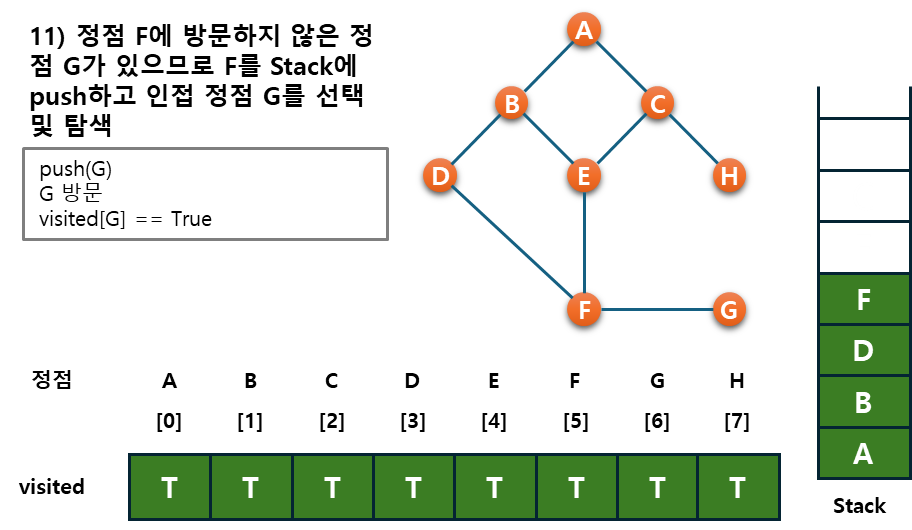
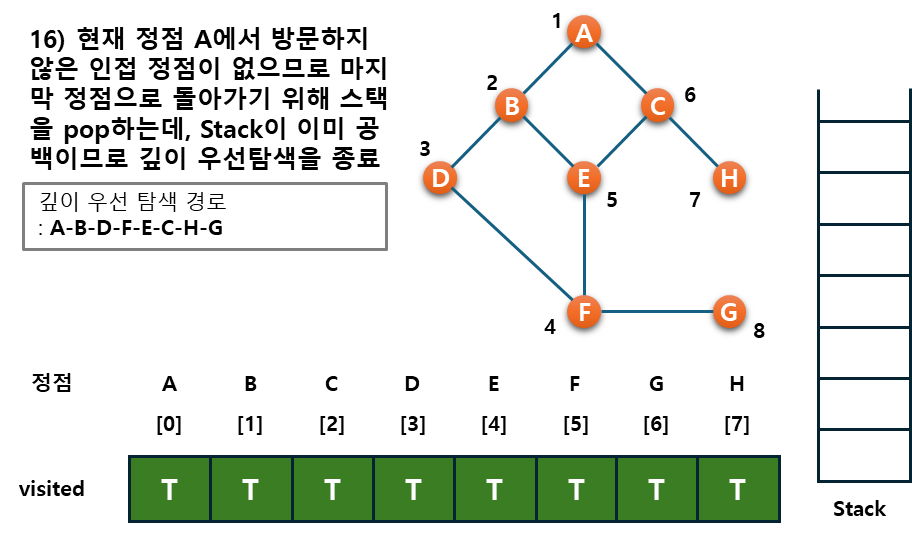
코드로도 살펴 볼까~~? 처음부터 시작하기 어려워서 일단은 GPT의 힘을 빌려 input 데이터 가공하는 법(문제 풀기위함)과 dfs의 자체 알고리즘을 천천히 살펴보면서 내 맛에 맞게 제작하였다.

def build_graph(input_data):              # graph 데이터 가공

    graph = {}                                       # 빈 딕셔너리 선언

    pairs = input_data.split()                # input_data에 따라 달라짐, 문자열로 진행

    for i in range(0, len(pairs), 2):        # 짝수번째 데이터만 가져오고 인덱스를 통해 데이터를 나눈다

        node = pairs[i]                            # 노드 정의

        neighbors = [pairs[i+1]]              # 노드와 연결된 이웃

        if node not in graph:                   # 새로 노드가 정의 됐다면 데이터 추가

            graph[node] = []                      # 빈 리스트로 넣으며

        graph[node].extend(neighbors)  # 데이터가 추가되면 {'a' : [b, c]} 의 형태를 띈다

    return graph                                    # 가공된 graph 데이터를 return한다.

def dfs(graph, start_node, end_node, path = None):  # DFS 함수 정의 path = None은 길을 못찾았다는 의미(재귀 위함)

    if path is None:                                    # 길 탐색을 위한 path list 초기화

        path = []

    path = path + [start_node]                  # 가장 처음 노드를 리스트에 추가해준다

    if start_node == end_node:                # 재귀하면서 start_node가 바뀌는데, end_node와 같아진다면

        return path                                     # return path를 통해 경로 자체를 가져온다

    if start_node not in graph:                  # 막다른 길을 만나면

        return False                                   # None을 반환하여 되돌아가게 한다

    for node in graph[start_node]:           # dict 데이터에서 연결된 neighbors 탐색

        if node not in path:                        # path에 없다면 (중복되지 않았다면) 다음 노드에서 새로운 길 탐색을 위한 재귀

            new_path = dfs(graph, node, end_node, path) # 이부분 이해가 어려움... ㅠㅠ

            if new_path:

                return new_path

    return None

input_data = '0 1 0 2 1 4 1 3 4 8 4 3 2 9 2 5 5 6 5 7 7 99 7 9 9 8 9 10 6 10 3 7'  # 들어올 그래프 데이터

start_node = '0'                                    # 시작 노드

end_node = '99'                                   # 종료 노드

graph = build_graph(input_data)         # 그래프 (dict 표현)

path = dfs(graph, start_node, end_node)   # 경로 탐색

print(path)                                            # ['0', '1', '4', '3', '7', '99']

 

 

파이참으로 순서를 돌려가며 이해했지만, 잘못된 길을 들었을 때 되돌아오는 부분이 조금 어렵게 느껴졌다. new_path 부분인데, 조금 더 공부해봐야겠다.