티스토리 뷰
블로그 작성하다가 초기화 됐다.. 슬프다..
bit를 미루고 미루다가 부분집합 부분을 풀면서 내가 사용하는 방식이 시간초과가 자주 뜨길래 이제는 미룰때까지 미뤘다 생각하여 bit를 이용한 연산에 도전하려 한다. 잘하는 친구들 보면 이미 비트연산을 자유롭게 사용하던데(특히 코드에 시프트 연산자 >> <<가 있으면 정말 멋있더라) 나도 멋있어져야지!
bit (비트)
: 컴퓨터에서 가장 작은 데이터의 단위이며 이진수 체계에서 0 또는 1의 값을 가진다. 한개의 비트는 0 과 1의 두가지 상태만 표현할 수 있다.
: 오른쪽부터 index 체계를 따라 0번부터 시작하고 8개의 비트가 있다면 가장 오른쪽 0번 비트부터 가장 왼쪽 7번 비트까지 존재한다.
8 bit를 묶으면 1Byte라고 한다.
하나의 예시를 들어보자 100011011011100은 몇 비트이면서 몇 바이트일까?

비트연산
:컴퓨터 CPU는 0과 1로 동작하며 내부적으로 비트 연산을 사용하여 사람이 사용하는 사칙연산(+, -, *, / ) 을 컴퓨터가 사용하는 연산인 '비트연산'으로 코딩할 수 있다. 그때 아래의 특징들이 있다.
- 빠른 연산속도
하드웨어 수준에서 직접 지원되기 때문에 연산이 더 빠르게 수행된다. 특히 속도가 중요한 대규모 데이터, 반복적인 연산에서 일반적인 산술보다 성능이 우수하다
- 메모리 사용 감소
데이터를 저장할 때 필요한 메모리 공간을 줄일 수 있다. 예를들어 여러개의 상태를 표현할 때(존재하는지 안하는지) 각 상태를 비트의 조합으로 표현하면 메모리의 사용량을 줄일 수 있다.
- 비트 단위 조작
데이터의 가장 작은 단위 비트 단위 조작을 가능하기 때문에 복잡한 데이터 구조를 다루거나 패턴 검색, 설정하는 등의 작업을 효율적으로 수행할 수 있다.
- 알고리즘 최적화
비트 연산을 활용하여 집합 연산(부분집합)을 수행하거나 그래프 알고리즘을 개선할 수 있다.
| 연산자 | 연산자의 기능 |
| & | 비트 단위로 AND 연산을 한다 두 개의 비트가 모두 1일 때 결과 비트가 1이 된다. 그 외에는 0이다. ex) num_a & num_b |
| | | 비트 단위로 OR 연산을 한다 둘 중 하나의 비트라도 1이라면 결과 비트가 1이 된다. 둘다 0이라면 0이다. ex) num_c | num_d |
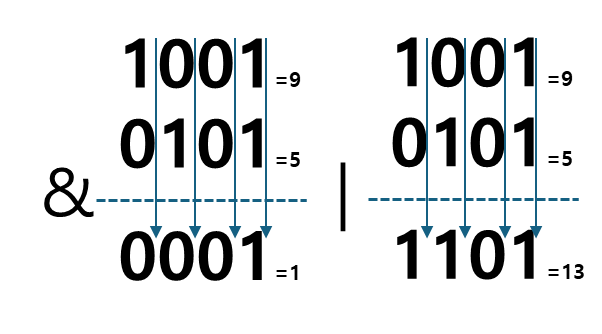
a = 0b1001
b = 0b101
print(a) # 9
print(b) # 5
print(a & b) # 1
print(a | b) # 13진법 변환
파이썬에서 2진수, 16진수, 10진수 자유자재 변경하기
먼저 N진수에서 10진수로 바꾸는 방법은 두가지가 있다.
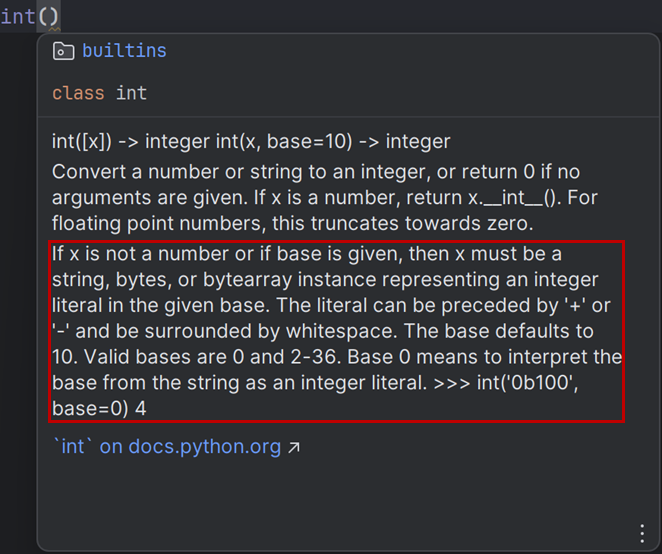
- int()를 보통 사용할 때 인자를 1개만 사용하는데, 문자열로 원하는 변형 N 진법의 수를 넣고 해당 진법 N을 기입해주면 10진법으로 바꿔준다.
- 혹은 각 진법을 10진법으로 표현하는 접두사(0b = 2진법, 0o = 8진법, 0x = 16진법)를 붙여 바로 바꿔줄 수 있다.
- 2진수는 숫자 0과 소문자 b(2진수 = binary)를 이용하여 0b를 접두사로 붙여 표현
print(0b10010) # 18
print(int('1100',2)) # 12- 8진수는 숫자 0과 소문자 o(8진수 = octal)를 이용하여 0o를 접두사로 붙여 표현
print(0o7424) # 3860
print(int('4526', 8)) # 2390- 16진수는 숫자 0과 소문자 x(16진수 = hexadecimal)를 이용하여 0x를 접두사로 붙여 표현
print(0xab4) # 2740
print(int('c7',16)) # 199
그렇다면 16진수를 다른 진수와 비트연산을 곧바로 가능할까? 도전해보자
a = 0b1001
b = 0xa
print(a) # 9
print(b) # 10
print(a & b) # 8
print(a | b) # 11
print(bin(a & b)) # 0b1000
print(bin(a | b)) # 0b1011
자동으로 binary로 변환 후 비트 연산을 진행하는 모습을 확인할 수 있다.
- 10진법을 각각 2, 8, 16진법으로 바꾸는 방법
N = 27
print(bin(N)) # 0b11011
print(oct(N)) # 0o33
print(hex(N)) # 0x1b
사실 내장 함수를 사용하지 않고, N진수의 경우 N으로 나눈 몫과 나머지를 찾아가며 가능하다. 편리한 방법과 불편한 방법 모두 알아두도록 하자.
# 10진수 -> N진수
# magic_table = {'0' : 0, dict를 이용한 N진수에서 10진수로 바꿀때
# '1' : 1,
# '2' : 2,
# '3' : 3,
# '4' : 4,
# '5' : 5,
# '6' : 6,
# '7' : 7,
# '8' : 8,
# '9' : 9,
# 'A' : 10,
# 'B' : 11,
# 'C' : 12,
# 'D' : 13,
# 'E' : 14,
# 'F' : 15}
magic_table = '0123456789ABCDEF' # 문자열의 인덱스를 이용한 10진수에서 16진수로 바꾸는 테이블
def convert(num, N):
remains = [] # 나머지들
while num != 0:
#몫과 나머지를 구하는 과정
num, remain = num // N, num % N
# 나머지는 remains 리스트에 저장
remains.append(remain)
for i in range(len(remains)):
remains[i] = magic_table[remains[i]]
return ''.join(remains[::-1])
print(convert(254, 16)) # EF
물론 데이터 리스트를 따로 생성해서 직접 넣어줘야하는 불편함은 있지만, 혹시나 내장 함수를 사용할 수 없는 상황이 온다면 위처럼 진행하면 된다. magic_table에 주석처리된 dictionary 형식보다 인덱스로 접근하는 magic_table이 좀 더 용이하다. (물론 시간복잡도를 따지게되면 차이가 조금은 있다)
XOR 연산
: 엑스오어 연산자, OR처럼 동작하나 둘 다 1인 경우는 0으로 바꾼다.
| 연산자 | 연산자의 기능 |
| ^ | 비트 단위로 XOR 연산을 한다. 같으면 0, 다르면 1이라고 생각하면 편하다 ex) num_e ^ num_f |
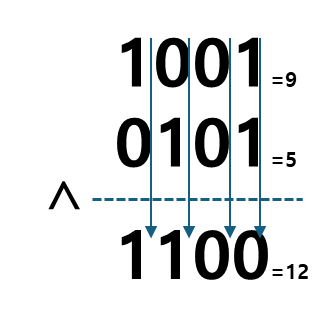
코드로 나타내면 아래와 같다
print(0b1001 ^ 0b0101) # 12
print(bin(0b1001 ^ 0b0101)) # 0b1100
여기엔 신기한 XOR 방식이 있다.
어떤 값이던 임의의 수로 2회 XOR 연산을 진행하면 원래의 수로 돌아온다.
마치 마술사가 내가 생각한 숫자 맞추는 기분인데, 궁금한건 못참지 실행해보자.
a = 624^1004
print(624^1004) # 412
print(a^1004) # 624
print((46143^1004)^1004)# 46143
그럼 이걸 어디다가 쓰는가?
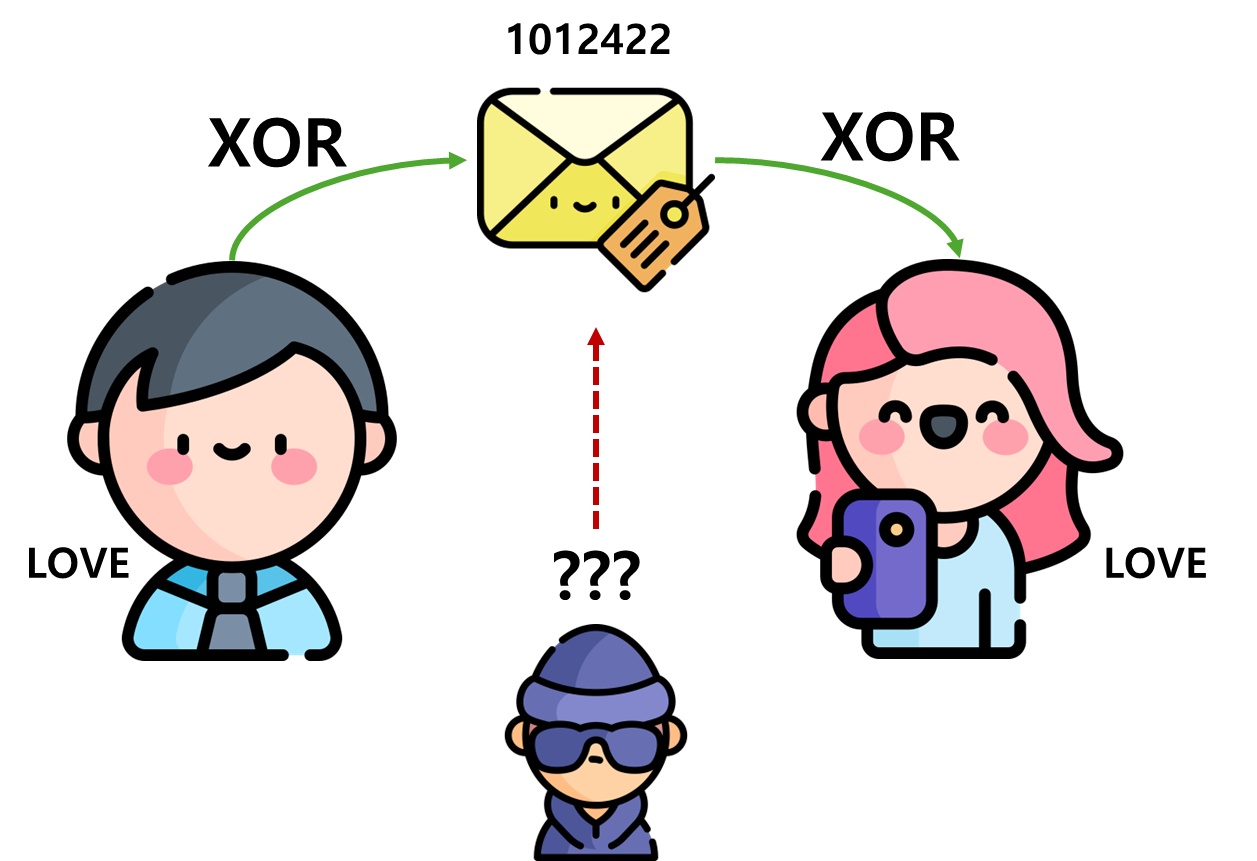
만약 내가 친구에게 특정 코드를 보내려고 한다고 하자. 하지만 다른사람들이 몰랐으면 좋겠어서 XOR연산을 하여 보냈다. 그렇다면 친구는 해당 코드를 알려면 어떻게 하면 될까? XOR연산을 한번 더 하면 본래의 코드로 돌아오는 것을 알 수 있다. 즉, 상대방과 내가 XOR 연산으로 암호화하는 비밀코드를 공유하고 있다면 다른 사람들이 해당 비밀코드를 맞추지 않는 한 추적할 수 없다.
# 10진법을 36진법으로 바꾸는 내장함수가 없기 때문에 앞서 배운 진법 변환을 사용한다
magic_table = '0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ'
def convert(num, N):
remains = []
while num != 0:
num, remain = num // N, num % N
remains.append(remain)
for i in range(len(remains)):
remains[i] = magic_table[remains[i]]
return ''.join(remains[::-1])
# 약속한 XOR 비밀코드를 1004라고 하자
i = 'LOVE'
code = int('LOVE',36) ^ 1004
print(code) # 1012422
# 상대방이 비밀코드를 1004라고 알고있다면?
decode = code ^ 1004
print(decode) # 1012010
print(convert(decode, 36)) # LOVE
#만약 XOR 비밀 코드를 모른다면?
what = code ^ 325
print(what) # 1012611
print(convert(what, 36)) # LPC3Shift 연산자 (Left와 Right)
- Left Shift (≪) : 특정 수 만큼 비트를 왼쪽으로 밀어낸다. (우측에 0이 생성된다)
- Right Shift (≫) : 특정 수 만큼 비트를 오른쪽으로 밀어낸다. (우측 비트들이 제거된다)
| 연산자 | 연산자의 기능 |
| ≪ | 피연산자의 비트 열을 왼쪽으로 이동시킨다. num_g << 2 # 우측에 0이 추가된다 |
| ≫ | 피연산자의 비트 열을 오른쪽으로 이동시킨다. num_h >> 2 # 우측에서 2개가 제거된다 |
파이썬 코드로 Shift 연산자를 확인해보자.
print(bin(0b1011 << 2)) # 0b101100
print(bin(0b101100 >> 3)) # 0b101
num = 1
for i in range(5):
print(bin(num), num, sep = ' : ')
num = num << 1
'''
0b1 : 1
0b10 : 2
0b100 : 4
0b1000 : 8
0b10000 : 16
'''
위는 Left Shift (≪)을 활용. 반복문을 통한 출력을 2진수와 10진수로 확인할 수 있다.
그럼 도대체 이 비트를 어디에 사용하는가??
i & (1 ≪ n)
조건문과 함께 쓰이면서 어디서 많이 본거같긴한데, 잘 모른다면 그때 그냥 넘어가서 일 것이다. 하지만 그 고비를 넘어야 할 때가 왔다.
- i의 n번 비트가 1인지 아닌지를 확인할 수 있다.
ex) if 1101 & (1≪2): 의 연산으로 1101에서 2번 bit가 1인지 확인한다
1 << ≪2 = 100임을 알 수있고 다음 연산인 1101 & 100(AND 연산은 둘다 1이면 1을 출력한다)을 하게되면 0100이 결과가 나오게된다. 즉 0이 아니기 때문에 n번 비트는 1임이 확정된다. 이것을 조건식의 boolen 타입으로 판단하게되면 조건문에서 True를 나타낼 수 있다.
반대로 if 1101 & (1 ≪ 1):라면 1101&10 = 0000 으로 값이 0이 되기 때문에 조건문에서 False임을 알 수 있다.
비트의 음수 표현 방법
: 비트에서 음수는 '2의 보수'를 사용하여 표현할 수 있다
- 맨 앞자리(최상위) bit (MSB = Most Significant Bit)는 음수 or 양수를 구분하는 비트이다
- MSB : 1이라면 음수, MSB : 0이라면 양수
예를들어 8비트 이진수 10110101 에서 가장 왼쪽 비트인 1은 MSB이다.
- 뺄셈의 연산 속도를 올릴 수 있으며, +0 과 -0을 따로 취급하지 않기 위해 사용한다
- 일반적으로 사용되는 정수 자료형은 8비트, 16비트, 32비트, 64비트 등이 있는데, 보통 컴퓨터의 아키텍쳐의 워드 크기와 관련이 있다. 이때 8비트는 각각이 2진수 비트 8개로 이루어진 byte를 나타내며, 여기에 부호 비트를 포함하여 최상상위 1비트는 부호를 나타내고 나머지 7비트는 값을 나타내는 것이다
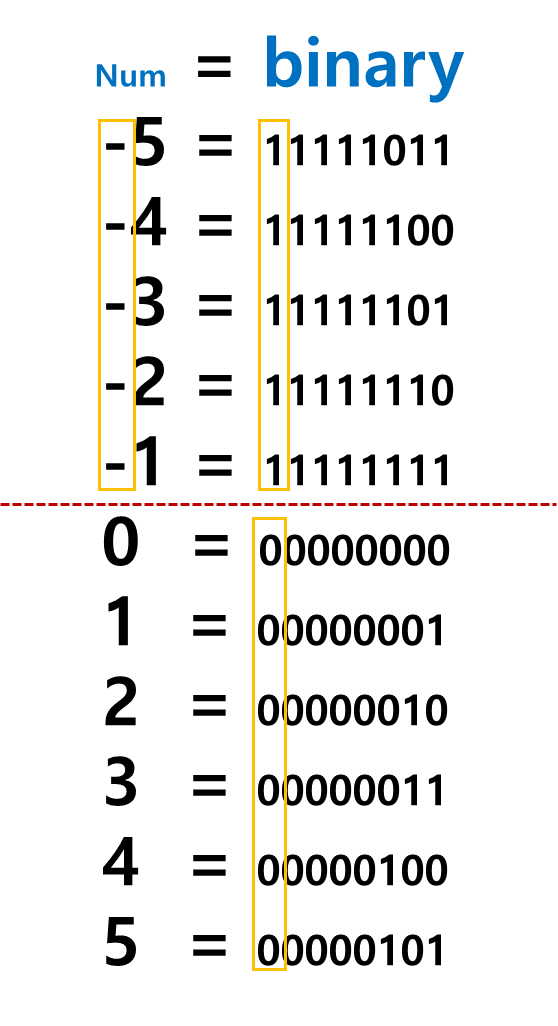
2의 보수 예시를 살펴볼 건데, 총 단계는 3개로 간단하니 차근차근 해보자.
비트의 음수표현으로 -5를 만들어 보자.
- 양수의 5를 비트표현으로 만든다.
- 5는 이진수로 0b00000101
- 모든 비트를 뒤집어준다.
- 0b00000101 에서 0b11111010으로 뒤집힌다.
- 1을 더해준다. 그 결과가 2의 보수이다.
- 0b11111010 + 1 : 0b11111011 이며 2의 보수 표현을 완료했다
여기서도 신기한 2의 보수가 있다.
2의 보수를 취한 수를, 한번 더 2의 보수를 취하면 원래의 값으로 돌아온다. 들었으면 한번 만들어야하지 않을까? 가보자고. (근데 사실 양수를 음수로 만드는 과정이었으니 반대로하면 당연히 돌아오는거 아닌가..?)
0b00010101 의 2의 보수로 만들어보자
뒤집기 : 0b11101010
더하기 : 0b11101011
2의 보수 결과인 0b11101011을 다시 2의 보수로 만들어보자
뒤집기 : 0b00010100
더하기 : 0b00010101
NOT 연산자
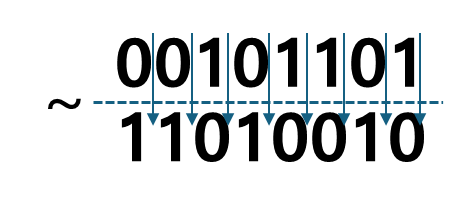
: (~) NOT 연산자 : 모든 비트를 반전시킨다
ex) 8bit 00101101을 뒤집는다면 ~(0010 1101) 이라면 결과는 1101 0010 이 된다.
print(~4) # -5
print(bin(~4)) # -0b101
print(~-4) # 3
print(bin(~-4)) # 0b11
간단하게만 정리하려했는데, 어쩌다보니 많이 길어진 것 같다. 가장 중요한 것은 if i & (1 ≪ n) 인 것 같다. 나중에 풀이하다가 꼭 써먹을 일이 있길 바라며!
'일상코딩 > 노트' 카테고리의 다른 글
| Python : 순열(Permutation) Review (2) | 2024.02.28 |
|---|---|
| Python : 반복(Iteration)과 재귀(Recursion) Review (0) | 2024.02.27 |
| Python : 트리 (Tree) (3) | 2024.02.20 |
| Python : 완전 탐색(= Brute-Force) Review (2) | 2024.02.15 |
| Python : Stack (2) [백트래킹, Backtracking] (1) | 2024.02.14 |
- Total
- Today
- Yesterday
- baby-gin
- Sequence types
- SQLite
- ssafy
- views.py
- 함수
- basic syntax
- Python
- Method
- ChatGPT
- 연산자
- 재귀
- 백준
- Component
- app
- vue
- honeymoney
- vue3
- Authentication System
- 순열
- Database
- CodeTree
- HTML
- SQL
- refactoring
- Django
- 카운팅정렬
- 삼성청년SW아카데미
- JavaScript
- dfs
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
